¿QUE ES ESTADÍSTICA?
Es la Ciencia que
estudia la recolección, análisis e interpretación de datos, ya sea para ayudar
en la resolución de la toma de decisiones o para explicar condiciones regulares
o irregulares de algún fenómeno o estudio aplicado, de ocurrencia en forma
aleatoria o condicional, es además, el vehículo que permite llevar a cabo el
proceso relacionado con la investigación científica.
Campos de la
estadística
·
Estadística descriptiva: se dedica a los métodos
de recolección, descripción, visualización y resumen de datos originados a
partir de los fenómenos de estudio. Los datos pueden ser resumidos numérica o
gráficamente. Ejemplos básicos de parámetros estadísticos son: la media y la
desviación estándar. Algunos ejemplos gráficos son: histograma, pirámide
población, entre otros.
·
Estadística inferencial: se dedica a la
generación de los modelos, inferencias y predicciones asociadas a los fenómenos
en cuestión teniendo en cuenta la aleatoriedad de las observaciones. Se usa
para modelar patrones en los datos y extraer inferencias acerca de la población
bajo estudio. Estas inferencias pueden tomar la forma de respuestas a preguntas
si/no (prueba de hipótesis), estimaciones de características numéricas (estimación),
pronósticos de futuras observaciones, descripciones de asociación (correlación)
o modela miento de relaciones entre variables (análisis de regresión). Otras
técnicas de modela miento incluyen. series de tiempo y minería de datos.
➤Muestra y Población
Población se refiere al universo, conjunto o totalidad de elementos sobre
los que se investiga o hacen estudios. Muestra es una parte o
subconjunto de elementos que se seleccionan previamente de una población para
realizar un estudio.
Normalmente se selecciona la muestra de una población para su estudio,
debido a que estudiar a todos los elementos de una población resultaría muy
extenso y poco práctico.
➤Población
|
➤Muestra
|
|
Definición
|
Universo de elementos que se van a
estudiar.
|
Selección de una parte de la
población que se va a ser sujeto de estudio.
|
Características
|
Se puede clasificar según la cantidad de
individuos que la conforman.
Posee variables estadísticas. |
Forma parte de la población: debería comprender
entre 5% y 10% para ser más efectiva.
Los elementos deben ser aleatorios.
Debe ser representativa de la población.
|
Objetivos
|
Analizar los datos recabados referentes a las características comunes
que comparten los elementos con diversos propósitos.
|
Estudiar el comportamiento, características, gustos o propiedades de
una parte representativa de la población.
|
Ejemplos
|
Las personas que habitan un país.
La cantidad de carros en una ciudad.
Los estudiantes de un país.
|
Para el estudio del desempeño de los estudiantes de cinco
universidades de una ciudad en una materia específica, se toma como muestra a
500 estudiantes aleatoriamente (100 de cada institución) que estén cursando
el mismo nivel para que la muestra sea representativa.
|
➤Varianza
La varianza es una medida de la dispersión de una variable aleatoria (valores que se obtienen de manera aleatoria). Es amplia mente utilizada en el área de estadística expresando, a través de un número, la variabilidad de dicha dispersión.
La varianza de una muestra se simboliza como S2, mientras que la varianza de una población de simboliza como σ2.
La varianza de una muestra es utilizada para estimar la varianza de una población, la cual en muchas ocasiones se desconoce. Es por esto que S2 también es considerada comúnmente como un estadístico y σ2 como un parámetro.
La varianza de una muestra presenta la siguiente fórmula:
S2 =
En cambio, la varianza de una población presenta la siguiente fórmula:
σ2 =
Si aun tienes dudas acerca de la varianza poblacional te dejamos un vídeo tutorial del calculo de la misma utilizando la formula anterior
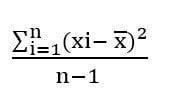
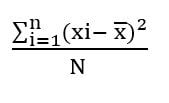
No hay comentarios.:
Publicar un comentario